CLASE N 12
1 DE FEBRERO DEL 2017
DISTRIBUCIONES DE MUESTREO
En esta sección se establecen algunas definiciones y términos relacionados con el estudio de la Estadística Inferencial que constituye el componente fundamental del estudio de la Estadística.
Una inferencia estadística es una afirmación que se hace acerca de algún parámetro de la población utilizando la información contenida en una muestra tomada de esta población.
Debemos aceptar que por la naturaleza aleatoria de los datos obtenidos en la muestra, hay un riesgo en la certeza de la afirmación propuesta, y es necesario establecer una medida para determinar la magnitud de este riesgo.
Supongamos una población de tamaño N de la cual se toma una muestra de tamaño n, obteniéndose los siguientes resultados: x1, x2, ..., xn
DISTRIBUCIÓN DE MUESTREO DE LA MEDIA MUESTRAL
Si el tamaño N de la población es finito y este número no es muy grande con respecto al tamaño n de la muestra, se debe usar la siguiente fórmula para corregir la varianza muestral, la cual se aplica si el tamaño de la muestra es mayor al 5% del tamaño de la población.
TEOREMA DEL LÍMITE CENTRAL
Con carácter general, o al menos en los modelos de probabilidad clásicos, se admite como una aproximación aceptable al modelo Normal siempre que n≥25, y se dice que la muestra es “grande”. Adicionalmente en este caso, si se desconoce la varianza de la población se puede usar como aproximación la varianza muestral: σ 2 ≅ S2
NOTA: El Teorema del Límite Central no implica que la distribución de la variable X tiende a la Distribución Normal a medida que n crece. El teorema establece que la distribución de la variable Z tiende a la Distribución Normal Estándar cuando n crece.
CLASE N 13
3 DE FEBRERO DEL 2017
NO HUBO CLASES POR LA NOVATADA
CLASE N 14
8 DE FEBRERO DEL 2017
LA DISTRIBUCIÓN JI-CUADRADO
Esta distribución se la obtiene de la distribución gamma. Tiene forma tipo campana con sesgo positivo. Se puede demostrar que si X es una variable aleatoria con distribución normal, entonces X2 es una variable aleatoria con distribución ji-cuadrado. Este hecho explica la importancia de la distribución ji-cuadrado en problemas de muestreo de poblaciones con distribución normal. Una aplicación práctica es la estimación de la varianza poblacional.





Esta distribución se la obtiene de la distribución gamma. Tiene forma tipo campana con sesgo positivo. Se puede demostrar que si X es una variable aleatoria con distribución normal, entonces X2 es una variable aleatoria con distribución ji-cuadrado. Este hecho explica la importancia de la distribución ji-cuadrado en problemas de muestreo de poblaciones con distribución normal. Una aplicación práctica es la estimación de la varianza poblacional.
EN DONDE EL SECTOR QUE CORRESPONDE A ALFA ES EL NIVEL DE SIGNIFICANCIA Y EL SECTOR 1-ALFA ES E NIVEL DE CONFIANZA
ESTIMACIÓN POR INTERVALOS
INTERVALOS DE CONFIANZA
El nivel de confianza de un intervalo mide la confiabilidad del método utilizado para calcular el intervalo. Un intervalo de confianza de un nivel 100(1 α)% se calcula mediante un método que a la larga dará como resultado que la media poblacional se sitúe en una proporción 1 α todas las veces que se utilice.
CLASE N 15
10 DE FEBRERO DEL 2017
INTERVALOS DE CONFIANZA PARA LAPROPORCION
: Es la proporción de la muestra.
X: El número de éxitos en n eventos.
n: Número de eventos o experimentos.
ñ: Es una ligera modificación de n para mejorar el intervalo de confianza.
: Es una ligera modificación de para mejorar el intervalo de confianza.
∝: Nivel de significación.
100(1-∝)%: Nivel de confianza.
Sea X el número de éxitos en n ensayos de Bernoulli independientes con probabilidad de éxito p, por lo que X~Bin(n, p).Se define ñ=n+4 p̃ =(X+2)/ñ y el estimador de p es =X/n. Entonces para un nivel de confianza de 100(1-α)%, un intervalo de confianza para p es :

La t de student
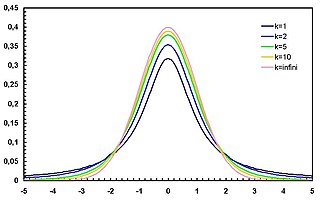
En probabilidad y estadística, la distribución t (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.
Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos medias muestrales y para la construcción del intervalo de confianza para la diferencia entre las medias de dos poblaciones cuando se desconoce la desviación típica de una población y ésta debe ser estimada a partir de los datos de una muestra.
La distribución t de Student es la distribución de probabilidad del cociente
donde
- Z es una variable aleatoria distribuida según una normal típica (de media nula y varianza 1).
- V es una variable aleatoria que sigue una distribución χ² con grados de libertad.
- Z y V son independientes
Si μ es una constante no nula, el cociente es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad .

CLASE N 16
15 DE FEBRERO DEL 2017
SOLO SE REALIZARON EJERCICIOS EN FORMA DE REPASO
Se hizo una encuesta a 325 personas mayores de 16 años y se encontró que 120 iban al teatro regularmente . Halla con un nivel de confianza del 94 % un intervalo para estudiar la proporción de los ciudadanos que van al teatro regularmente.
Los métodos de interpolación se usan para calcular las alturas sobre el nivel del mar para ubicaciones donde las mediciones directas no están disponibles. En un artículo se evalúa un método de promedio ponderado de interpolación para calcular las alturas de mediciones GPS. El método se estableció para interpretar errores “grandes” (errores cuya magnitud están por encima de umbral comúnmente aceptado) en 26 de 74 ubicaciones de prueba. Determine un intervalo de confianza de 90% para la proporción de ubicaciones en las que este método tendrá errores grandes.
El número de éxitos es X = 26
El de ensayos n =74
Por tanto, se calcula:
ñ = 74+ 4 = 78
Para un intervalo de confianza de 90%, el valor de α/2 es 0.05, por lo que
El intervalo de confianza de 90% es, por tanto,
















No hay comentarios:
Publicar un comentario