DICIEMBRE

CLASE N 12

2 de diciembre del 2016

tuvimos la evaluacion 2

CLASE 13

7 de diciembre del 2016

Eventos independientes

Sean A y B eventos cualesquiera de un espacio muestral S. Se dice que A y B son independientes si P(A|B) = P(A) y P(B|A) = P(B), es decir que el evento A no depende del evento B y el evento B no depende del evento A

A y B son eventos independientes si P(A∩B) = P(A) P(B)

Ejemplo. 

Calcule la probabilidad que el último dígito del número de una placa de carro elegida al azar sea par y el penúltimo dígito sea impar

Sean los eventos

A: El último digito es par

B: El penúltimo dígito es impar

Cada evento no está relacionado con el otro evento, entonces son independientes.

Por lo tanto,

P(A∩B) = P(A) P(B) = 0.5 x 0.5 = 0.25

En este tipo de eventos es muy importante considerar si son un muestreo con reposición o no.

Ejemplo 1.

En una caja hay 10 baterías de las cuales 4 están en buen estado. Se repite dos veces el siguiente ensayo: extraer una batería al azar, revisar su estado y devolverla a la caja.

a) Encuentre la probabilidad que en ambos intentos se obtenga una batería en buen estado.

La primera batería se toma de la caja y se la devuelve, entonces el evento B no es afectado por el resultado que se obtuvo en el evento A, por lo tanto son eventos independientes.

P(A∩B) = P(A) P(B) = 0.4 x 0.4 = 0.16

b) Calcule la probabilidad que en los dos intentos se obtenga al menos una batería en buen estado

Con la conocida Fórmula Aditiva de Probabilidad,

P(A∪B) = P(A) + P(B) – P(A∩B) = 0.4 + 0.4 – 0.16 = 0.64

Ejemplo 2. 

En una caja hay 10 baterías de las cuales 4 están en buen estado. Se extraen al azar dos baterías sin devolverlas a la caja. 

REGLA MULTIPLICATIVA DE LA PROBABILIDAD

Sean A, B eventos no nulos cualquiera de S, entonces

Definición: Regla Multiplicativa de la Probabilidad

P(A∩B) = P(A) P(B|A)

a) La probabilidad que ambas baterías estén en buen estado es P(A∩B), pero los eventos

A y B no son independientes. Entonces con la fórmula anterior

P(A∩B) = P(A) P(B|A)=0.1333

La probabilidad de éxito del evento A es 4/10. Para el evento B la probabilidad de éxito es 3/9, dado que A es favorable (quedan 3 baterías en buen estado del total de 9 baterías)

b) La probabilidad que una batería esté en buen estado y la otra en mal estado:

P(A∩Bc) + P(Ac∩B) = P(A)P(Bc|A) + P(Ac)P(B|Ac)= (4/10)(6/9) + (6/10)(4/9) = 12/15 = 0.5333

Los eventos que solamente la primera batería esté en buen estado y que solamente la segunda batería esté en buen estado son excluyentes, por lo tanto sus probabilidades se suman:

c) La probabilidad que al menos una esté en buen estado. Con los resultados de en a) y b):

P(A∪B) = P(A∩B)∪P(A∩Bc

)∪P(Ac

∩B) = 2/15 + 8/15 = 2/3 =0.6666

Los eventos que ambas estén en buen estado o que solamente una esté en buen estado son mutuamente excluyentes, por lo tanto sus probabilidades se suman.

d) La probabilidad que ninguna esté en buen estado

P((A∪B)c) = 1 – P(A∪B) = 1 – 2/3 = 1/3 = 0.3333

Es el complemento del evento que al menos una esté en buen estado.

CLASE N 14
9 DE DICIEMBRE DEL 2016

En este día se realizaron ejercicios como repaso para el examen.

Ejercicio 1:

En el juego de 40 se reparten 5 cartas al azar a cada jugador, a partir de un aso de 40 cartas cual es la probabilidad de que el jugador tenga

a)Un A, 2, 3, 4 ,5del mismo palo:

(probabilidad de a) = (Probabilidad de que salga A) (Probabilidad que salga un 2 del mismo palo)(Probabilidad que salga un 3 del mismo palo)(Probabilidad que salga un 4 del mismo palo)(Probabilidad que salga un 5 del mismo palo)

(probabilidad de a) =4/40 . 1/39 . 1/38 . 1/37 . 1/36

b)salgan 4 cartas del mismo palo

(probabilidad de b) =  (Probabilidad que salga una carta del mismo palo)(Probabilidad que salga una carta del mismo palo)(Probabilidad que salga una carta del mismo palo)(Probabilidad que salga una carta del mismo palo)

(probabilidad de b) =1/40 . 9/39 . 8/38 . 7/37

c)salga una ronda

(probabilidad de c) =(Probabilidad que salga una carta del mismo simbolo)(Probabilidad que salga una carta del mismo simbolo)(Probabilidad que salga una carta del mismo simbolo)

(probabilidad de c) = 4/40 . 3/39 . 2/38

Ejercicio 2

Una empresa tiene 2 tiendas que vende en el norte y en el sur, de los cuales se sabe que el 30% solo compra en el norte, el 50% compra en el sur, el 10% indistintamente en cualquiera de las 2 tiendas y el otro 10% no compra en ninguna

	A	Ac	Total
B	10	50	60
Bc	30	10	40
Total	40	60	100

a) P(A) = 40/100

b) P(AUB)= 90/100

c) P(Bc)=40/100

d) P(A∩B)=1/100

e) P(A/B)=1/6

f) P(Ac∩Bc) =10/100

g) P(A∩Bc)=90/100

h) P(AUBc)=50/100

En este ejercicio se demostró que es mas fácil trabajar con la tabla de doble entrada que con el lenguaje de los conjuntos

Ejercicio N 3

En la intersección de una autopista los automóviles pueden girar a la D o a la I desde un puesto del observador y se registran los movimientos de los 3 primeros vehículos

Para este ejercicio es de mucha facilidad realizar el diagrama de árbol ya que no es posible realizar una tabla de doble entrada

SEGUNDO BIMESTRE

CLASE 1

14 DE DICIEMBRE DEL 2016

VARIABLES ALEATORIAS DISCRETAS

• En el material estudiado anteriormente aprendimos a calcular la probabilidad de eventos de un
• espacio muestral S. En esta unidad estudiaremos reglas para establecer correspondencias de
• los elementos de S con los números reales, para luego asignarles un valor de probabilidad.

Ejemplo.

En un experimento se lanzan tres monedas y se observa el resultado (c: cara o s: sello).

El conjunto de posibles resultados (espacio muestral) para este experimento, es el siguiente:

S = {( c, c, c),( c, c, s),( c, s, c),( s, c, c),( c, s, s),( s, c, s),( s, s, c),( s, s, s)}

X: Variable aleatoria (número de sellos que se obtienen)

Las Variables Aleatorias establecen correspondencia del espacio muestral S al conjunto de los números reales. Esta correspondencia es funcional y se la puede definir formalmente.

Al realizar el experimento, se obtendrá cualquier elemento del espacio muestral S.

Por lo tanto, la variable aleatoria X puede tomar alguno de los números: 

x = 0, 1, 2, 3.

Las variables aleatorias pueden representarse con las letras mayúsculas X, Y, ...

Para un mismo espacio muestral S pueden definirse muchas variables aleatorias.

Para el ejemplo de las 3 monedas, algunas otras variables aleatorias sobre S pueden ser:

Y: Diferencia entre el número de caras y sellos

Z: El número de caras al cubo, mas el doble del número de sellos, etc.

Para cada variable aleatoria el rango es un subconjunto de los reales. Según el tipo decorrespondencia establecida, las variables aleatorias pueden ser discretas o continuas.En el ejemplo de las monedas, X es una variable aleatoria discreta pues su rango es un subconjunto de los enteros. Además es finita.

DISTRIBUCIÓN DE PROBABILIDAD DE UNA VARIABLE ALEATORIA DISCRETA

FUNCIÓN DE DISTRIBUCIÓN DE PROBABILIDAD

HISTOGRAMA DE DISTRIBUCIÓN DE PROBABILIDAD

Distribución Acumulada para Variables Aleatorias Discretas

Propiedades de la Distribución Acumulada para Variables Aleatorias Discretas

1) 0 ≤ F(x )≤1 F es una función de probabilidad
2) a ≤ b ⇒ F(a) ≤ F(b) F es creciente
3) P(X>a) = 1 – P(X≤a) = 1 – F(a) Complemento de Probabilidad

CLASE 2

16 DE DICIEMBRE DEL 2016

MEDIA Y VARIANZA DE UNA VARIABLE ALEATORIA DISCRETA

MEDIA:

PROPIEDADES:

VARIANZA:

PROPIEDADES

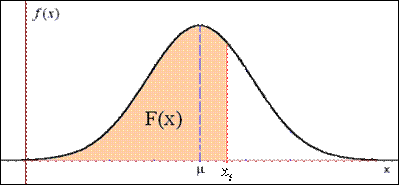
VARIABLES ALEATORIAS CONTINUAS

Una variable aleatoria es continua si sus probabilidades están dadas por áreas bajo una curva. La curva se llama función de densidad de probabilidad para la variable aleatoria.

A veces la función de densidad de probabilidad se llama distribución de probabilidad.

DISTRIBUCIÓN DE VARIABLES ALEATORIAS CONTINUAS

CLASE N 3
21 DE DICIEMBRE DEL 2016

FUNCIÓN DE DENSIDAD DE PROBABILIDAD

PROPIEDADES:

Ejemplo

Suponga que el tiempo de atención de cada cliente en una estación de servicio es una variable aleatoria continua con la siguiente función de densidad de probabilidad:

a) Verifique que cumple las propiedades de una función de densidad

Sea X: variable aleatoria continua (duración en horas)

b) Calcule la probabilidad que el tiempo de atención esté entre 15 y 30 minutos

FUNCIÓN DE DISTRIBUCIÓN

Al igual que en el caso discreto se puede definir una función de probabilidad acumulada, la cual en el caso continuo se denomina función de distribución

Encuentre la función de distribución para el ejemplo anterior

Use la Función de Distribución para calcular P(1/4<X<1/2) en el ejemplo anterior